Binary Space Partitioning
There's an excellent GDC 2011 presentation with Tom Hall and John Romero (writer/designer and designer/programmer) that explains where BSPs came from; GDC Vault - Classic Game Postmortem - DOOM (The "Work on Doom Resumed" part).
The problem Doom faced during development was that it would consider every line in the world for rendering; quite the massive loop to perform if your level has many sectors with many walls. The solution is to remove as much data as possible from that loop and only loop over the visible data to figure out what the player is looking at - BSP is just one way to do that.
BSP itself is unrelated to the rendering of Doom. It is a culling optimisation performed offline to generate a tree to discard data and leave a list of walls that are visible from any point on the map.
The Algorithm

This is E1M1 as seen in the Doom Builder map editor. The BSP compiler will recursively slice this level to generate a tree, with the root representing the entire level. The slice-points are chosen by roughly finding the line closest to the middle of the current branch (a branch is a collection of sectors).
The chosen lines are always ones that connect two sectors, so sectors can be separated into "infront of the line" and "behind the line". The compiler will also split the map-editor sectors into convex subsectors to remove the need to store draw-order information. Joel "Bisqwit" Yliluoma explains the reason for this perfectly in his video Creating a Doom-style 3D engine in C - the short explanation is that you can see all the walls around you if you're standing in a convex subsector and there won't be any walls behind other walls.
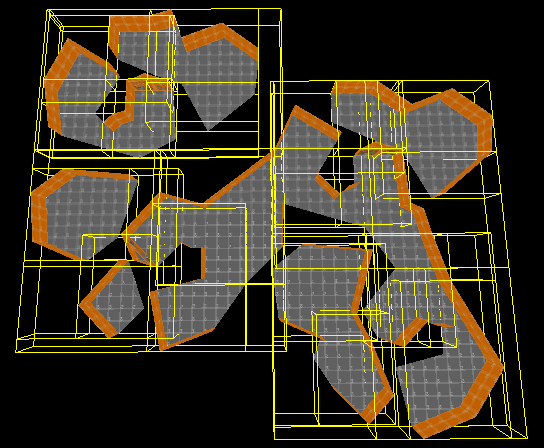
Bounding boxes are generated to help discard sectors during rendering. This is pretty much standard practise for most 3D renderers these days. The image above is an old BSP rendering project I wrote a while ago showing the bounding boxes of a load-time compiled map.
All this happens in 2D space, however the BSP technique can be applied to maps with 3D-space and has been used in many, many 3D games since Doom.
Runtime
Doom optimises the rendering step by having it piggy-back off of the occlusion crawl step. This is actually similar to Wolfenstein 3D and ray-casting (as well as most software-rendered games), where ray-casting is technically a visibility occlusion algorithm, but Wolfenstein 3D uses this to draw the walls at the same time, rather than store the data and defer the rendering for later (which is how a traditional 3D scene-graph works).
The BSP compiler also generated lists of visible line segments for each of the subsectors. This means that a subsector will literally have a list of all the walls that can potentially be seen from any point inside it. Doom just needs to figure out what subsector you're in by traversing the BSP tree, then it can draw whatever is on that list.
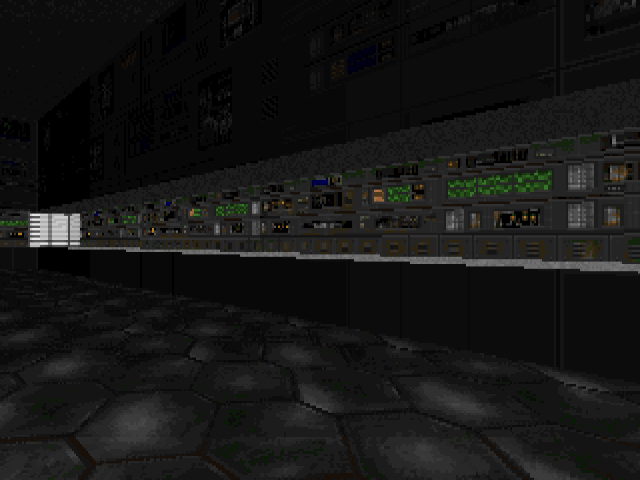
In the editor, this section of wall in E1M1 is a single linedef.

In engine, the BSP compiler has split this section of wall into multiple lines (shown by the multiple colours along the wall) and each of these line segments belong to a convex subsector.
Tree Traversal
This is where BSP is used to figure out where the player is so we can work out what they are looking at.
The root-branch of the BSP tree is a line that is hopefully near the middle of the map. Half the map is on one side, the other half is on the other side - if we know what side of the line we're on, then we can discard half the map (more-or-less) from the visibility search on step 1.
The next node on the tree should be a line where roughly quarter of the remaining map is on one side, and quarter on the other and the process repeats. Eventually the algorithm will hit a leaf node that has no split (leaves at the end of branches). The leaves are subsectors, so what we're left with is the only possible subsector that the player is within.
/*====================
r_defs.h
====================*/
typedef struct subsector_s {
sector_t * sector; /* Parent sector information */
short numlines; /* How many line segments are potentially visible */
short firstline; /* Offset into the list of line segments */
} subsector_t;
typedef struct lineseg_s {
vertex_t * v1;
vertex_t * v2;
/* ... */
side_t * sidedef; /* Line segments only care about one side of the line */
line_t * linedef; /* Parent line information */
sector_t * frontsector;
sector_t * backsector; /* NULL for single-sided lines */
} seg_t;
typedef struct bspnode_s {
/* BSP partition line */
fixed_t x;
fixed_t y;
fixed_t dx;
fixed_t dy;
fixed_t bbox[2][4]; /* BSP bounding box for children */
unsigned short children[2]; /* BSP front and back children */
/* testing children[2] against the constant NF_SUBSECTOR defines a leaf */
} node_t;
#define NF_SUBSECTOR ( 0x8000 )
Subsectors contain a list of visible wall segments, so clip those walls against the camera and then draw them to the screen. These walls are sorted near to far by the BSP generation, so no draw-order calculation is required at this stage, we can guarantee that the nearest wall will be correct and we can clip the next wall in the list against that and so-on until the entire list is clipped and/or rendered.
Rooms Above Rooms
This is both a limitation with the map data that Doom uses and the renderer, however I wrote a bit about y-sheering over in the rendering section so the room-above-room problem is going here.
On your first play-through of Doom you'll probably never notice that there are no second-floors to any of the rooms. There's also no floating platforms or real bridges (they all seem to extend from the floor). You'll never notice this until you look at the maps in a level editor, and then you'll never be able to unsee it because it is a pretty obvious limitation when you know what to look for.
Doom probably could have attempted these features by packing more meta-data into the sectors and linedefs, but there's a limit to how much space you can cram onto a floppy-disk and the maps were complicated enough with only 1 floor to work with, adding an extra floor may make things a little too complicated to design around. It also gives more work for the engine to do and computer processors in the early 90s didn't exactly have the wiggle-room to handle more complexity.Doom probably didn't need multiple floors anyway.
All that said; How can we have multiple floors? Marathon did it, Duke Nukem 3D did it and Dark Forces did it, so surely it's possible?
Portal Rendering
Marathon's renderer is fantastic. The C++ source code is pretty crazy and the engine itself can be incredibly buggy ("humpy polls" - for those of you in the loop). Here's a map that has two floors on top of each other, on the same level (wtf?).
A top-down view of the map doesn't explain anything. Luckily for us Bisqwit once again saves the day with another fantastic video.
This is Bisqwit's showcase of a Duke Nukem 3D map achieving non-euclidean geometry (the fancy name for 5D-space).
It's not hard to imagine one of these rooms being up a winding staircase, thus giving the illusion that a room is on-top of another room. Bisqwit also has a few videos of this affect in a modern game, Portal 2, so subscribe to his YouTube channel and check out his videos.
Doom source ports and Dark Forces
There's one last bit of craziness to this room-over-room story. The Sonic fan-game Sonic Robo Blast 2 uses a modified Doom engine and features roofs on top of buildings that you can stand upon. Furthermore, LucasArts' Star Wars: Dark Forces also has something like this in some levels for bridges.


Both of these games likely achieve this with lots of meta data about these particular cases. Dark Forces in particular features 3D models, so some extra data about "bridge height" and a 3D model resolves that case. Sonic Robo Blast 2 has a lot of custom meta-data for levels, likely there's a "bridge lower height" and "bridge upper height" value somewhere for this special case.